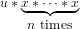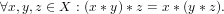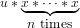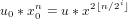12 MyBinaryPowering
The basic idea of binary powering is to construct the result by considering the
exponent in binary expansion. There are two methods: process the binary expansion
of the exponent from left to right (from the highest to the lowest bit) or from right to
left. The left-to-right version is very simple. We cite from [Knu69] and note that n
has to be a positive integer.
Write n in the binary system (suppressing zeros at the left). Then
replace each “1” by the pair of letters SX, replace each “0” by S, and
cross off the “SX” which now appears at the left. The result is a rule
for computing xn, if “S” is interpreted as the operation of squaring,
and if “X” is interpreted as the operation of multiplying by x.
The right-to-left variant is a bit more complicated but more appropriate for our
purpose. The main reason why we decide for the right-to-left variant is that for a
destructive version we do not require the underlying domain to have a copy
function.
82⟨* 13⟩+
≡ ⊲58b 89 ⊳
-------------------------------------------------------------------
----
---- ALLPROSE
---- Copyright (C) Ralf Hemmecke (ralf@hemmecke.de)
---- http://www.hemmecke.de/aldor
----
-------------------------------------------------------------------
#assert DontNeedLibraryMyAlps
#include "myalps"
⟨pkg: MyBinaryPowering 84⟩
Uses DontNeedLibraryMyAlps 37.
Type Constructor
MyBinaryPowering
Usage
x: X := binaryPower(67, 22, 7) $ MyBinaryPowering(X, *$X, N);
y: X := binaryPower(67, 22, 7) $ MyBinaryPowering(X, +$X, N);
Parameters
-
X: Type
-
The type of elements that should be exponentiated.
-
*: (X, X) -> X
-
An associative operation; for example, multiplication or addition on
X.
-
N: BinaryRepresentedNumberType
-
A natural-number-like type for the exponents where
-
-
macro BinaryRepresentedNumberType == with {
zero?: % -> Boolean;
one?: % -> Boolean;
length: % -> MachineInteger;
bit?: (%, MachineInteger) -> Boolean;
}
We tacitly assume that no negative elements are passed as the third argument
to binaryPower. In fact, there is no concept of negative here. Elements of N
are only interpreted through their length and their bits. Typical candidates for
N are Integer and MachineInteger.
Description
Binary exponentiation.
MyBinaryPowering provides an implementation of a binary exponentiation algorithm
for the domain X with exponents in N. In fact, since the only requirement on the
operation *: (X, X) -> X is associativity, there is no restriction of this package to
just computing binaryPower(u,x,n) = u⋅xn. For example, if X and N are Integer,
then for the x and y from above it holds: x = 67 ⋅ 227 = 167121978496 and
y = 67 + 22 ⋅ 7 = 221.
84⟨pkg: MyBinaryPowering 84⟩≡ (82)
MyBinaryPowering(
X: Type,
*: (X, X) -> X,
N: with {
zero?: % -> Boolean;
one?: % -> Boolean;
length: % -> MachineInteger;
bit?: (%, MachineInteger) -> Boolean;
}
): with {
⟨exports: MyBinaryPowering 86⟩
} == add {
TRACEINSTANTIATION;
⟨implementation: MyBinaryPowering 88⟩
}
Defines:
MyBinaryPowering, used in chunk 89.
Uses TRACEINSTANTIATION 36.
Exports of MyBinaryPowering
-
-
binaryPower: (X, X, N) -> X Returns the first argument times the second argument
raised to the power given by the third argument.
Export of MyBinaryPowering
binaryPower: (X, X, N) -> X
Usage
macro {
X == MachineInteger;
N == Integer;
}
import from MyBinaryPowering(X, * $ X, N);
u: X := 1;
x: X := 22;
n: N := 7;
r: X := binaryPower(u, x, n);
Parameters
-
u: X
-
The element to multiply to the power.
-
x: X
-
The element to exponentiate.
-
n: N
-
The exponent.
Description
Returns the first argument times the second argument raised to the power given
by the third argument.
binaryPower(u, x, n) computes
by a
binary powering algorithm where the operation
*: (X, X) -> X can be any
associative operation, i. e.,
Typical examples are multiplication and addition.
Remarks
The package MyBinaryPowering implements the function binaryPower in terms of
a given function *: (X, X) -> X. The function * is allowed to destroy or reuse its
first argument. If * is destructive then binaryPower destructively modifies its
first and second argument. If * is non-destructive then binaryPower is
non-destructive.
Also read the description of MyBinaryPowering about negative exponents, i. e., for
negative values of elements of N.
86⟨exports: MyBinaryPowering 86⟩≡ (84)
binaryPower: (X, X, N) -> X;
In the following we are going to implement the right-to-left variant of the binary
exponentiation algorithm, i. e., we process the exponent beginning with the lowest
bit.
The implementation does not have access to a neutral element of the
operation *: (X, X) -> X. In fact, there might not even exist a neutral element.
Furthermore, if the operation *: (X, X) -> X works destructively on its first
argument, we would need some additional storage anyway. That is the reason
why we only provide a function with arguments u, x, n in order to compute
instead of just giving the parameters x and n.
The algorithm given below certainly returns the correct result if n = 0 or
n = 1.
For the correctness of the algorithm for n > 1 note that in the loop just after the
statement
the invariant 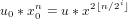 |
(1)
|
holds where u0, x0, and n are the input parameters and u, x, and i are the values
at that point of the computation. If i = s then ⌊n∕2i⌋ = 0 and consequently,
u0 ∗ x0n = u.
Note that by the required signature of the package parameter N there is actually
no direct way to really compute ⌊n∕2i⌋. However, since N is considered in a binary
representation, the value ⌊n∕2i⌋ is just the number n where the lowest i bits have
been cut off.
Additionally note that we have used the short-hand xn to really mean
88⟨implementation: MyBinaryPowering 88⟩≡ (84)
binaryPower(u: X, x: X, n: N): X == {
macro I == MachineInteger;
zero? n => u;
one? n => u*x;
i: I := 0;
s: I := length n;
assert(s > 1);
repeat {
if bit?(n, i) then u := u * x;
i := i + 1;
i = s => return u;
x := x * x;
}
never;
}